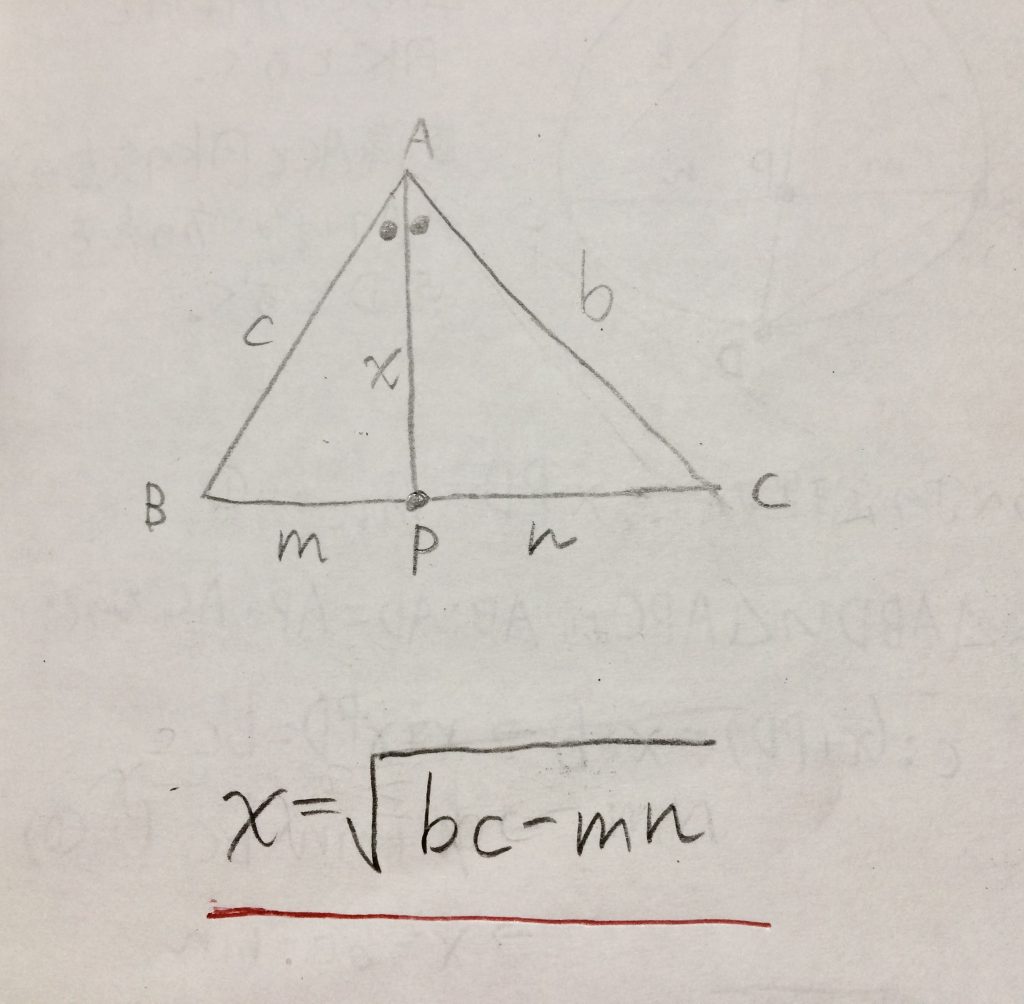〜No insects, No life.〜
前回の県模試で、引き算で盛大にミスったので、
もはや、引き算特訓システムみたいなのを、自分で作ってみるか
って思って、desmosで作りました。
僕は、なんでも自分でやるまで気が済まない性格なので、
夢中で作っちゃいました。
これを使って、引き算特訓しようかな。
.
下記リンクを押すと、そのページが開きます。
https://www.desmos.com/calculator/duazbtdtft
デバイスによっては、文字が重なったりして、見にくくなる場合がありますが、
その時は、マウスをスクロールするか、指で画面を拡大してください。
頑張って、自力で、一般の累乗和の公式を導出しましたぁ。
和分差分・階乗冪・マクローリン展開の３つをうまく使いました。
↓つまり、こういうこと。
（終）
お久しぶりです。
今日は、数学の話題で。
角の２等分線について、上写真のような性質が知られています。
この性質は、一般的には、余弦定理とかを使って証明するんですが、
もっと面白い証明の仕方を思いついたので、ここに載せておきますね。
△ABCの外接円を考えることで、
三角比を一切使わずに、
三角形の相似だけを使って証明できちゃうんです！
（方冪の定理も、実質、三角形の相似）
なかなか面白い証明方法だと思います。
(終)
お久しぶりです、虫キョロリスです。
次は、昆虫の記事投稿しようかなあと言っておきながら、また、数学の話題で恐縮なんですが、、。(^_^;)
結構以前から、「立方体が回転する様子を、数式を使って、xy座標平面に表せないかなあ」って思ってたんですけど、
今回、実際にグラフ化することに成功したので、それについて書かせてください。
「desmos」というグラフ描画サイトを使って、書いてみました。
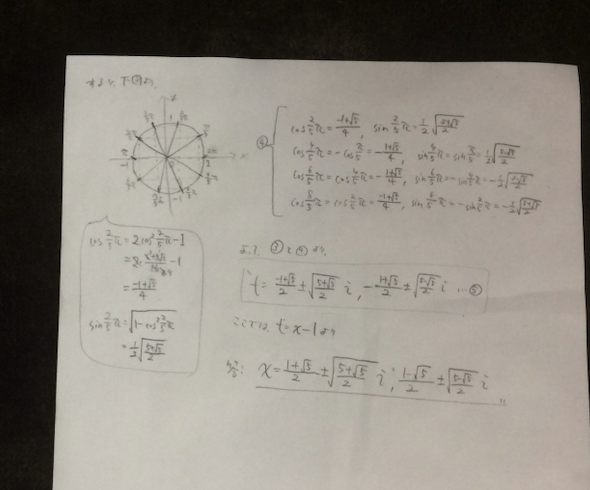
えっと、まあ、どうやって、数式作ったのかというのは、下の写真にまとめてみました。
見にくい部分とか、説明がわかりにくい部分があるのは、お許しを。。😅
結局、これで導き出した式
・x = l(cosθ1cosθ3-sinθ1sinθ2sinθ3)-mcosθ2sinθ3-n(sinθ1cosθ3+cosθ1sinθ2sinθ3)
・y = l(cosθ1sinθ3+sinθ1sinθ2cosθ3)+mcosθ2cosθ3+n(cosθ1sinθ2cosθ3-sinθ1sinθ3)
に、l,m,nの値を代入してって、作ればいいってこと！
…………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………
そして、この、僕の作ったグラフが、下記リンクから見れるので、是非見てってください！
なかなか綺麗だと思います。
前回出した、自作問題の答えです。
平行移動で、見慣れた四次方程式に持っていき、その後は、複素数の極形式を使って解いていきます。
もし、なんか間違ってるとこあったら、教えてください。
お久しぶりです。虫キョロリスです。
今日は、昆虫の話題ではなく、数学について書こうと思います。
今回、話題にするのは、次のような問題。
問. 平行六面体 ABCD-EFGHに関して、４つの対角線の中点が一致することを証明せよ。
空間ベクトルの典型的かつ基本的な問題です(^ ^)
一般的な解き方は、下の写真のような解き方だと思います。
う〜ん、真ん中の、｛ の部分、ちょいと わかりにくいですよねえ。
「aベクトル+gベクトル＝bベクトル+hベクトル」を示すためには、
「ABベクトル＝DCベクトル」や「ABベクトル＝EFベクトル」ではなく、
「ABベクトル＝HGベクトル」の組み合わせを使わないといけません。
それを逆算して考えるのが、若干分かりにくいように思います。
そこで、別の方法で解いてみました。
斜交座標の登場でっす！
う、、うつくしくないですか？！
厳密には、斜交座標でも中点の公式が使えること をちゃんと示さないといけないかもしれないけど。。。（でも、もし書くとしても、ちょっとの説明で証明できる）
やっぱり斜交座標、便利ですねぇ。
……………………………………………………………………………………………………………….
ついでに、最後に、最近僕が作った自作問題を置いておくので、
是非解いてみてください😁 （解答はまた後日）
