月: 2021年11月

前回出した、自作問題の答えです。

平行移動で、見慣れた四次方程式に持っていき、その後は、複素数の極形式を使って解いていきます。

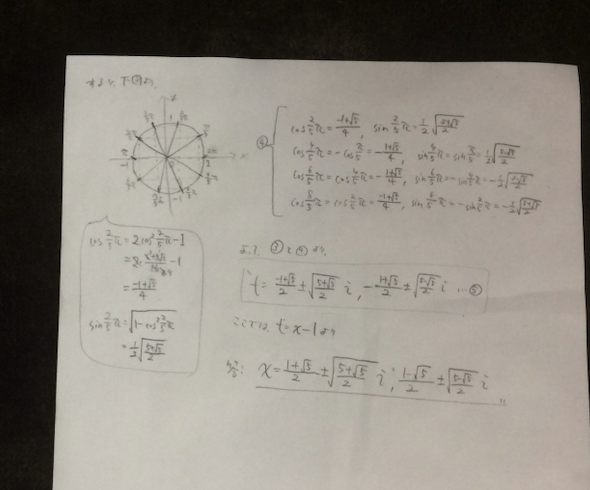
もし、なんか間違ってるとこあったら、教えてください。

お久しぶりです。虫キョロリスです。

今日は、昆虫の話題ではなく、数学について書こうと思います。

今回、話題にするのは、次のような問題。

問. 平行六面体 ABCD-EFGHに関して、４つの対角線の中点が一致することを証明せよ。

空間ベクトルの典型的かつ基本的な問題です(^ ^)

一般的な解き方は、下の写真のような解き方だと思います。

う〜ん、真ん中の、｛　の部分、ちょいと わかりにくいですよねえ。

「aベクトル+gベクトル＝bベクトル+hベクトル」を示すためには、

「ABベクトル＝DCベクトル」や「ABベクトル＝EFベクトル」ではなく、

「ABベクトル＝HGベクトル」の組み合わせを使わないといけません。

それを逆算して考えるのが、若干分かりにくいように思います。

そこで、別の方法で解いてみました。

斜交座標の登場でっす！

う、、うつくしくないですか？！

厳密には、斜交座標でも中点の公式が使えること をちゃんと示さないといけないかもしれないけど。。。（でも、もし書くとしても、ちょっとの説明で証明できる）

やっぱり斜交座標、便利ですねぇ。

……………………………………………………………………………………………………………….

ついでに、最後に、最近僕が作った自作問題を置いておくので、

是非解いてみてください😁　　（解答はまた後日）

ツトガ科ツトガ亜科。開張15〜20mm。

学名：Pseudargyria interruptella。

……………………………………………………………………………………………………….

今回は、ホソスジツトガという蛾です。

学名に、「interrupt（割り込む、中断する）」の文字が入ってるのが、

少し気になりますねぇ。

なんでなんでしょう？　

う〜ん？？？　わかんないや😅。

…

この子は、比較的よく見かけますが、

小さい蛾なので、あんまり注目されない種類かもしれないですね。

でも、

真っ白に透き通る翅と、

なめらかな曲線を描く金粉が、

ほんとうに魅力的です。

この曲線、見てるだけで心が和みますね。

金色という豪華な色を使いながらも、

翅の模様は決して派手なわけではなく、

清らかで、優しく穏やかな印象があります。

そして、

翅の外縁にある三対の黒い点。

なんか、この６つの黒点に、

ふと見つめられてるような気がしますねぇ。

（終）